Mục lục
Bài 1: Phương pháp đánh giá dịch bệnh, từ đó đưa ra các quyết định trong phòng chống dịch bệnh
Bài 2: Một phương pháp dự báo dịch bệnh [được chuyển đến đây từ link gốc đã xuất bản ngày 18/7/2021]
Phụ lục: Các bài phân tích làn sóng dịch Covid-19 thứ 4 từ 14/07 - 29/08
Một phương pháp dự báo dịch bệnh
Trong bài viết này chúng tôi đề cập đến bài toán dự báo. Dự báo một bệnh dịch là rất khó do có rất nhiều yếu tố khác nhau tác động đến bệnh dịch (RT). Nó nôm na như có nhiều yếu tố khác nhau tác động đến GDP trong kinh tế. Như CDC Mỹ dùng 26 mô hình của các nhóm nghiên cứu khác nhau, sau đó tổng hợp chúng lại thành một mô hình (được gọi là Ensemble) 1.
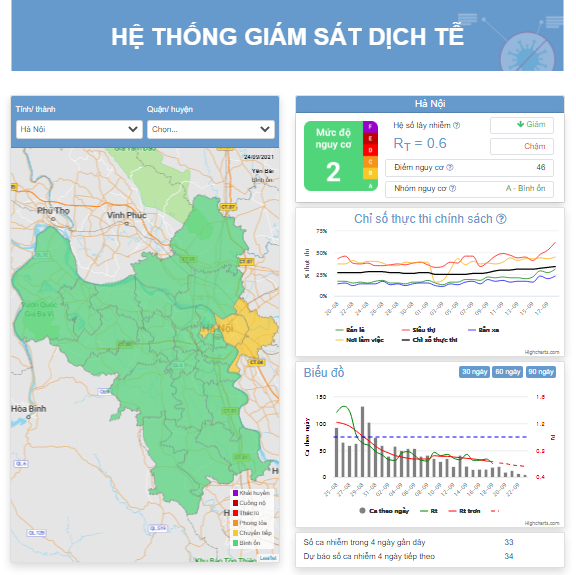
Trong bài cập nhật hàng tuần, vào trưa 15/7/2001, do RT hôm 14/7 là 1,66 và có chỉ thị 16 cho TP Hồ Chí Minh, chúng tôi đưa ra dự đoán thô là tổng số ca phát hiện trong 4 ngày 17/7 đến 18/7 sẽ gấp ít nhất 1,5 lần tổng số ca phát hiện trong 4 ngày 11/7 đến 14/7 trên Việt Nam. Tuy nhiên RT không tiếp tục đi xuống mà đi ngang, và dữ liệu hôm nay cho thấy con số trên là 1,7 (nếu làm trơn RT thì là 1,62). Trong bài này, chúng tôi sẽ đưa ra một phương pháp dự đoán khác phương pháp dự đoán thô.
Đầu tiên ta nói qua về phương pháp dự đoán thô. Nếu RT không thay đổi trong tương lai, thì số ca được phát hiện trong n*T ngày tương lai là (khi RT > 1)
(Số ca trong T hôm gần nhất) * RT * (RT n – 1)/( RT – 1).
Phương pháp này nhanh nhưng không tốt cho khoảng thời gian dài (n lớn). Vì lý do này, chung tôi trình bày một phương pháp khác cho phép dự báo xa hơn. Dựa trên dữ liệu chúng tôi có chỉ là số ca phát hiện mỗi ngày, và thuộc tính thời gian ủ bệnh của COVID-19, chúng tôi lựa chọn mô hình đơn giản nhất, đó là SEIR. Chúng ta cần thay đổi một số thứ khi áp dụng SEIR. Tập I trong SEIR sẽ đại diện cho số ca mới phát hiện trong vòng T ngày, tập E đại diện cho những ca chưa phát hiện. Cuối cùng chúng tôi sử dụng nhiều mô hình SEIR trên các khoảng thời gian liên tiếp thay vì chỉ một mô hình SEIR (hoặc SEIR với tham số phụ thuộc thời gian), nhằm đáp ứng việc hệ số lây nhiễm cơ bản thay đổi. Gọi t0 là thời điểm xuất phát sao cho nó trước hôm nay T = 4 hôm (do đó hôm nay là t0 + 4). Ta chọn t0 làm điểm xuất phát do ta cần dữ liệu ước lượng các tham số. Các tham số được dùng trong mô hình SEIR được liệt kê trong bảng sau (8 tham số).
|
Tham số |
Giá trị |
Lý do |
|
N: Tổng dân số Việt Nam |
98 triệu |
Xấp xỉ |
|
E0 : Số ca bệnh chưa được phát hiện hôm t0 |
Tổng số ca phát hiện từ t0 +1 đến t0 + 4 |
Đây là khoảng thời gian đa số những ca này được phát hiện |
|
I0 : Số ca bệnh được phát hiện trong vòng T ngày cho tới t0 |
Tổng số ca phát hiện từ t0 – 3 đến t0 |
|
|
Remove0: Số ca không liên quan quá trình lây bệnh |
1 triệu |
Không ảnh hưởng quá nhiều tới mô hình |
|
Gamma: Thời gian ủ bệnh trung bình |
4 ngày |
Thời gian ủ bệnh trung bình cho chủng Delta khoảng 4 ngày |
|
Delta |
4 ngày |
T |
|
Re |
Ước lượng của RT hôm t0 |
|
|
Beta |
Tính từ các tham số trên |
|
Ta cần RT để dự đoán số ca tương lai. Do việc dự đoán RT khó, chúng tôi đưa ra một số kịch bản trong bảng sau.
|
Tên |
RT |
Lý do |
|
Kịch bản 1 |
RT được ước lượng theo đường làm trơn (smooth spline với spar 0.6). |
Một cách ước lượng RT. |
|
Kịch bản 2 |
RT là hằng số, được ước lượng bằng giá trị hôm nay của đường làm trơn. |
Tình huống xấu khi ta dập dịch không hiệu quả, chỉ đủ duy trì tình hình hiện tại. |
|
Kịch bản 3 |
RT giảm tuyến tính từ giá trị ước lượng hôm nay (1,62) xuống 1.1 trong vòng 3 tuần (giảm 0,025/ngày). |
Dựa vào tình hình phong tỏa một số nơi trên thế giới, Bắc Giang, và Bắc Ninh, chúng tôi cho rằng đây là một viễn cảnh lạc quan. |
Do ước lượng của RT hiện nay gần như là hằng số nên chúng tôi bỏ kịch bản 1. Kết quả kịch bản 2 được biểu diễn trong các Hình 1 và 2. Trong Hình 1, ta thất bại và chỉ duy trì RT ở 1,62, khi đó dịch vẫn lên đỉnh sau khoảng 3 tháng rồi đi xuống. Tuy nhiên số ca được phát hiện lúc đỉnh dịch sẽ trên 1 triệu ca/ngày. Đường màu đỏ là số ca mắc mới. Số ca mắc mới nhiều hơn số ca được phát hiện trong giai đoạn đầu do có nhiều ca mắc mới ta chưa phát hiện ra. Điều này bị đảo ngược lại trong tương lai khi số người lành không mang bệnh giảm đi. Hình 2 là giới hạn của Hình 1 trong 21 ngày. Chỉ trong 13 ngày tới, tổng số ca được phát hiện đã gần 100 nghìn (chưa tính số ca chưa được phát hiện). Tổng số ca được phát hiện trong 21 ngày tới là 219.771.
Kết quả của kịch bản 3 trong Hình 3. Dù đây là kịch bản chúng tôi cho là lạc quan, chỉ trong 17 ngày tới, tổng số ca được phát hiện đã xấp xỉ 100 nghìn (chưa tính số ca chưa được phát hiện). Tổng số ca được phát hiện trong 21 ngày tới là 165.353.
Chi tiết về việc sử dụng compartmental model nói chung và SEIR nói riêng cho dự báo có thể được xem trong slide đính kèm trong bài viết trước và các tài liệu tham khảo được đề cập trong đó.
Tài liệu tham khảo
1. COVID-19 Forecasts: Cases | CDC. Available at: https://www.cdc.gov/coronavirus/2019-ncov/science/forecasting/forecasts-cases.html. (Accessed: 18th July 2021)
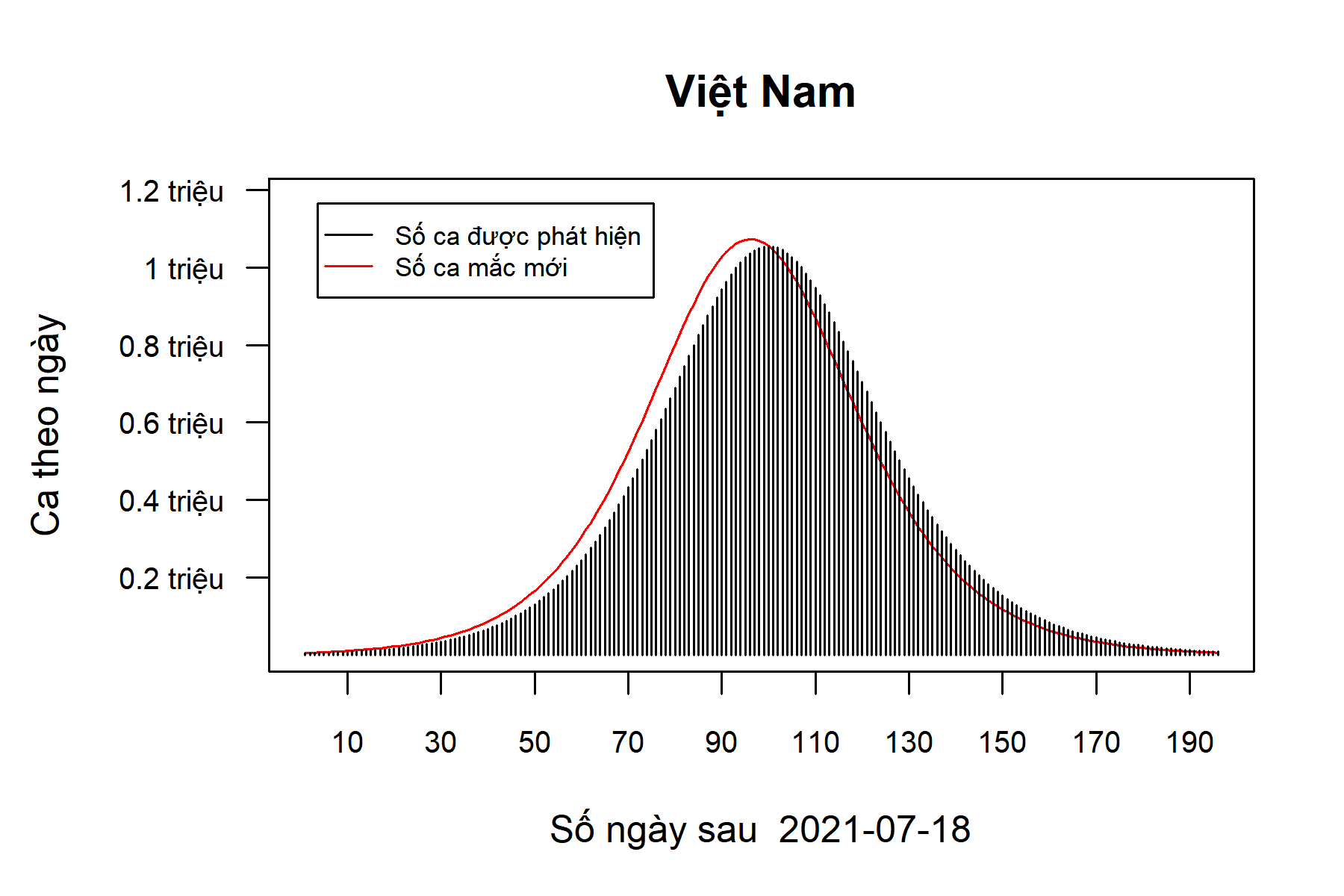
Hình 1. Kịch bản 2 với RT = 1.62.
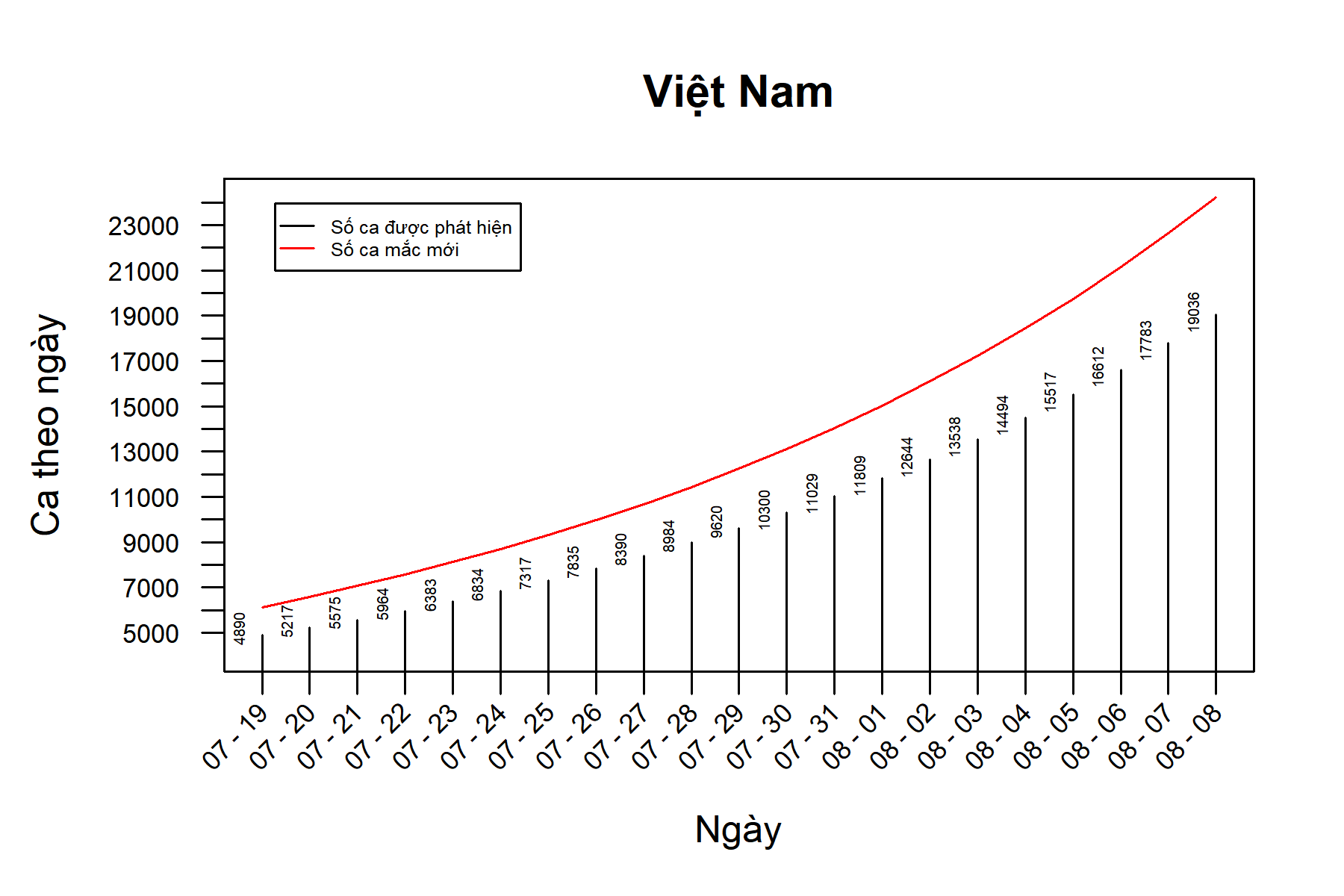
Hình 2. Kịch bản 2 với RT = 1.62 trong 21 ngày đầu tiên.
(Tổng số ca được phát hiện trong 21 ngày tới là 219.771.)
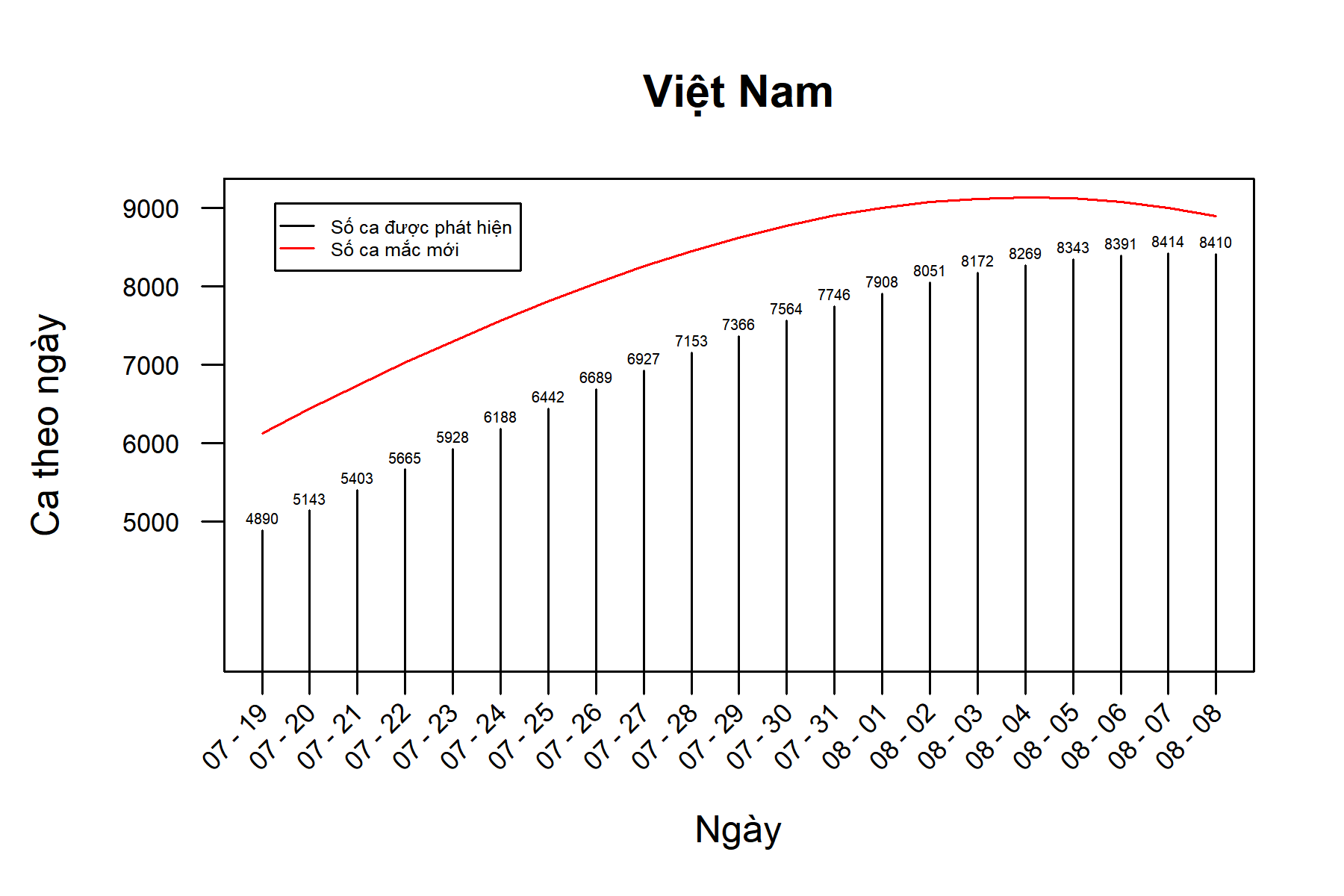
Hình 3. Kịch bản 3 với RT giảm tuyến tính từ 1.62 xuống 1.1 trong vòng 21 ngày (hay giảm 0.025/ngày)
(Sau 21 ngày gần bắt kịp dịch bệnh với 165k ca bệnh, đây là viễn cảnh lạc quan.)
Bình luận:
Chưa có bình luận nào.